【印刷可能】 連立 方程式 例題 112009

トップ100連立方程式公式 最高のカラーリングのアイデア
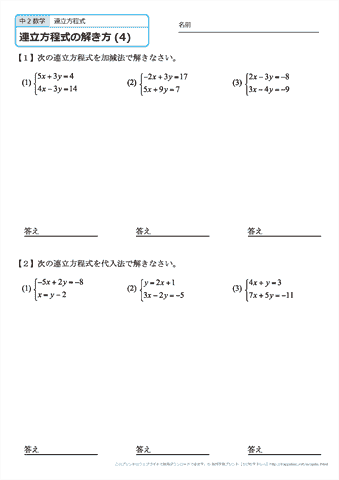
連立方程式(計算練習2) 連立方程式を解け y=2x3 3xy=4 5xy=13 4xy=11 5x3y=19 4xy=11 x3y=8 x2y=7 5xy=9 y=2x5 4x7y=1 3x2y=8 2x3y=10 x=y5 12x04y=2 21x04y=46 3(4x2y)=x9 2x3y=6 4 3 x 5 4 y= 1 2 3 2 x 3 4 y= 9 2 1 4 x 1 2 y=1 2 3 x 8 9 y= 4 9 4x3y=2xy6=2連立一次方程式①(掃き出し法) 例題を解きながら掃き出し法を用いて連立一次方程式を解く方法をコツとともにわかりやすく解説します。 解き方 掃き出し法は、拡大係数行列の簡約化をすることと一緒で
連立 方程式 例題
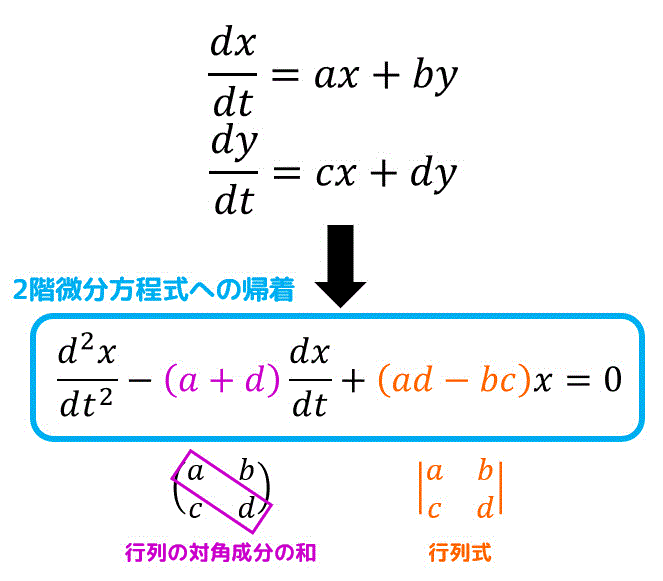
連立 方程式 例題- 連立方程式 複数の方程式が { でくくられたもの 全ての式をみたす値の組み合わせを 連立方程式の解 という 式が2つのものから100個のものまで連立方程式と呼びます。 ここでは2元1次方程式が2つあるものを扱っていきます。 例題をみてみましょう。分方程式は階数が上がると解くのが難しくなるので階数を下げて連立微分方程式の形に持ち込むということがよ くやられます。余談になりますが,一般に2 階線形微分方程式 d2x dt2 P1(t) dx dt P2(t)x = Q(x) を連立微分方程式にして階数を下げるには, x = x1;

高校数学で学習する連立方程式の解き方まとめ 数スタ
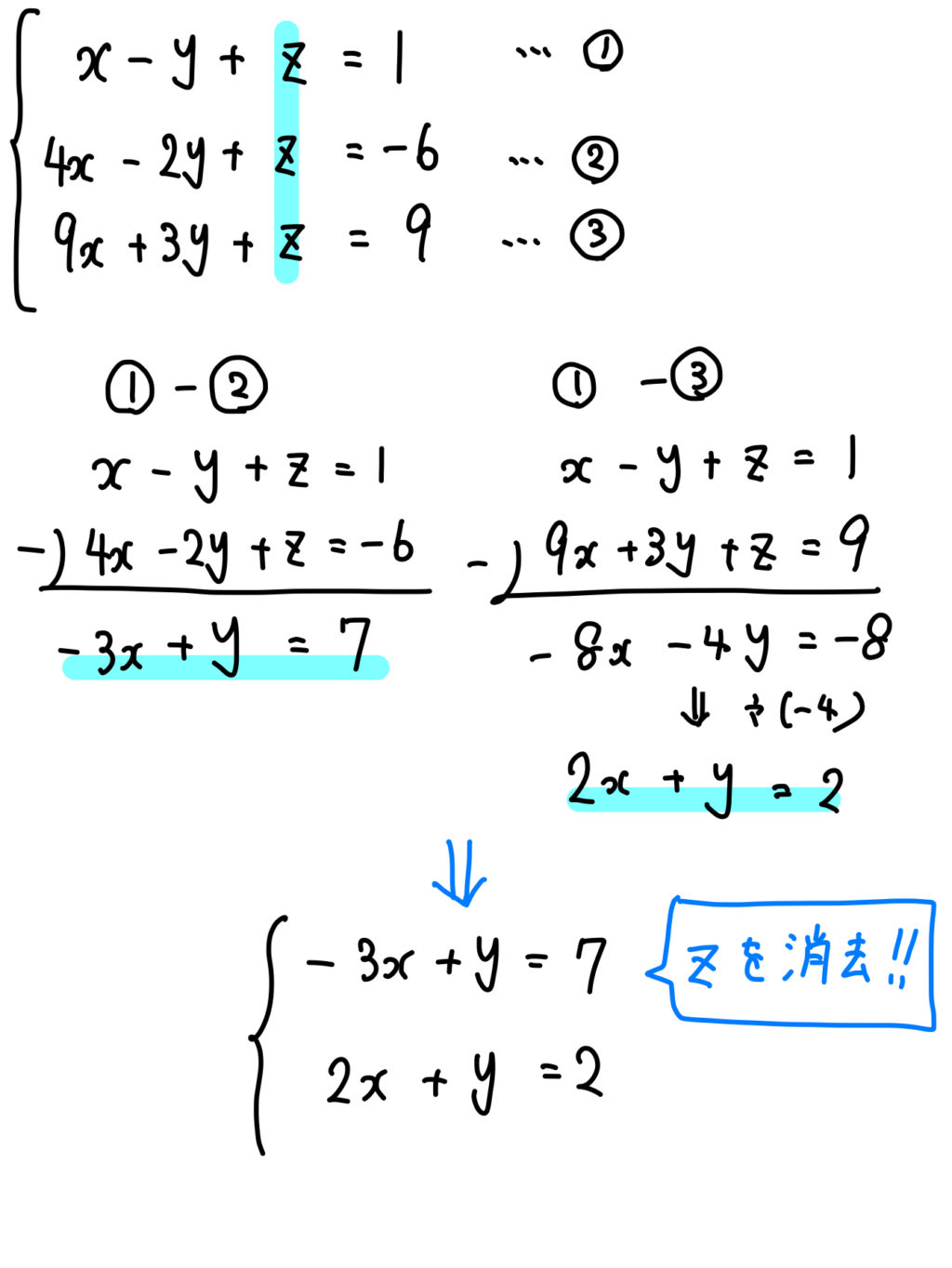
定数係数連立線形常微分方程式— 11 同次方程式 次の形の連立常微分方程式を定数係数連立線形常微分方程式とよぶ: は定数 この方程式を満たすベクトル をこの方程式の解と呼ぶ。 特に 常に の場合、即ち を同次斉次方程式とよぶ。 iv連立一次方程式 例題 以下に示す二元連立一次方程式を①ヤコビ法および②ガウス・ザイデル法で解け。 但し、初期値はx 1 = x 2 = 0、精度ε= 0005 とせよ。 2 2 5 2 4 1 2 1 = = x x x x 二つの方法での近似解の漸化式は以下の様になる。 ① ヤコビ法 () 1 ( ) 1 よって、連立方程式の解は $$(x,y,z)=(1,4,6)$$ となります。 解を求めるまで、長い道のりでしたが(^^;) まずは、文字を1つ消していつも通りの連立方程式を作るというのがポイントでしたね。 練習問題はこちら >準備中 連立方程式3つのまとめ!
連立方程式とは {7x2y =5 2x5y = 8 のように2つ以上の方程式を組み合わせたものが 連立方程式 である。 組み合わせた, どの方程式も成り立たせるような文字の値の組が連立方程式の解となる。 中学で扱うのは上記のような2元1次方程式の連立方程式である。 定価・原価・利益の問題(連立方程式) 問題文の中に、求める数が2つある場合は、それぞれを 、 で表します。 ただし、問題によっては、求める数に関連のある数を 、 としたほうが解きやすい場合もあります。 問題文から等しい関係にあるものを連立方程式の文章題(文字の置き方) <例題 > 携帯電話を購入し、60分間通話したら、購入代金と通話代金で、合わせて、6000円だった。 また、同じ携帯電話を購入し、1分間通話したら、購入代金と通話代金で、合わせて、9000円だった。 携帯電話の
連立 方程式 例題のギャラリー
各画像をクリックすると、ダウンロードまたは拡大表示できます
 |  | 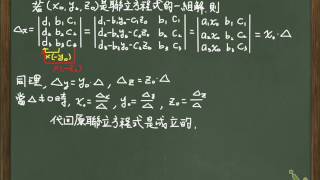 |
 |  |  |
 |  |  |
「連立 方程式 例題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
.png) |  |  |
「連立 方程式 例題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | 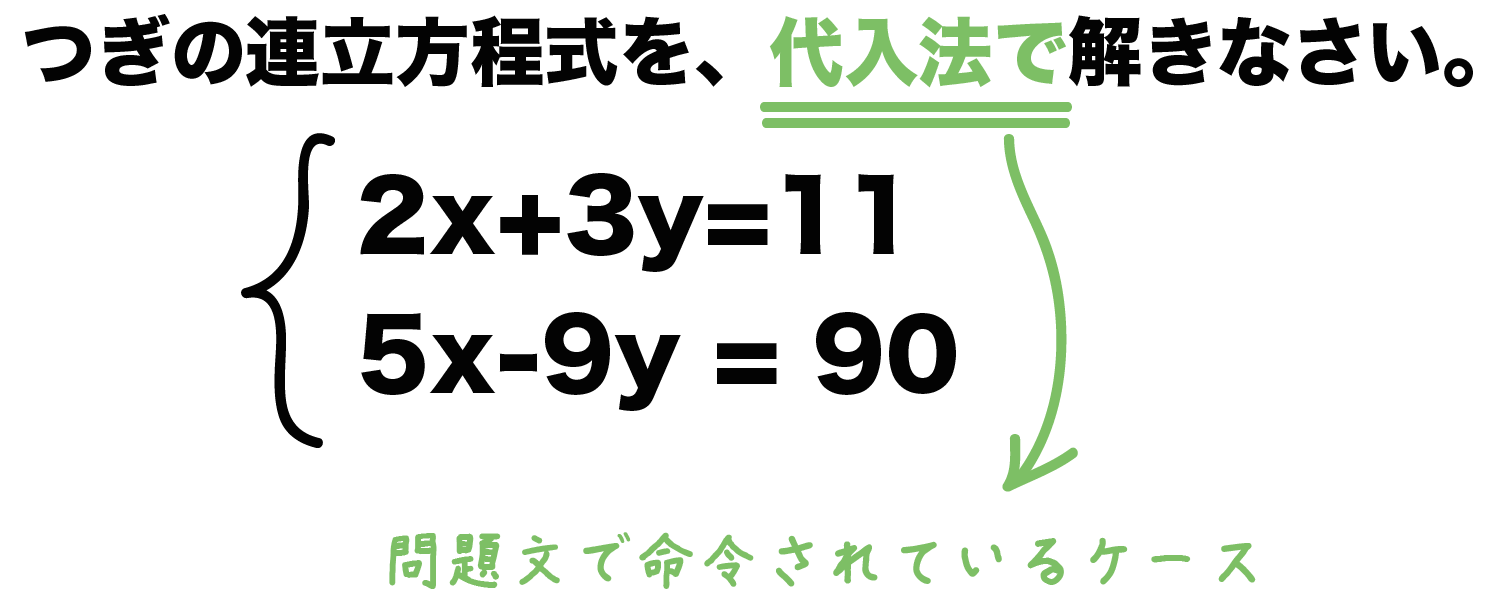 | |
「連立 方程式 例題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 | ||
「連立 方程式 例題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  |  |
 |  |  |
「連立 方程式 例題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  | |
 |  | |
 | 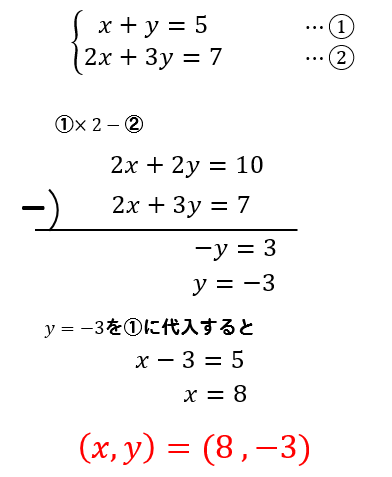 |  |
「連立 方程式 例題」の画像ギャラリー、詳細は各画像をクリックしてください。
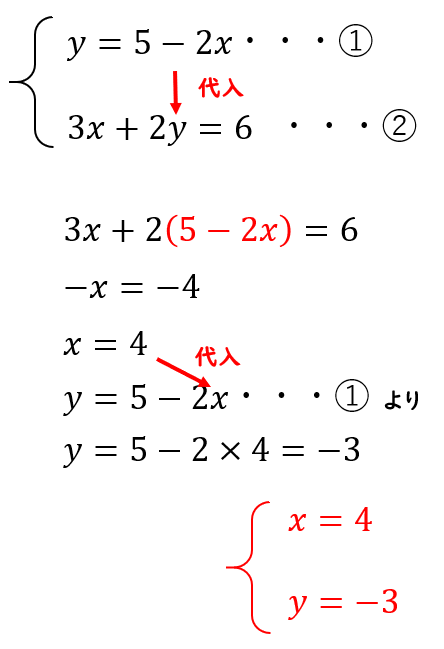 |  | |
 |  |  |
 |  | |
「連立 方程式 例題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | |
 |  |  |
「連立 方程式 例題」の画像ギャラリー、詳細は各画像をクリックしてください。
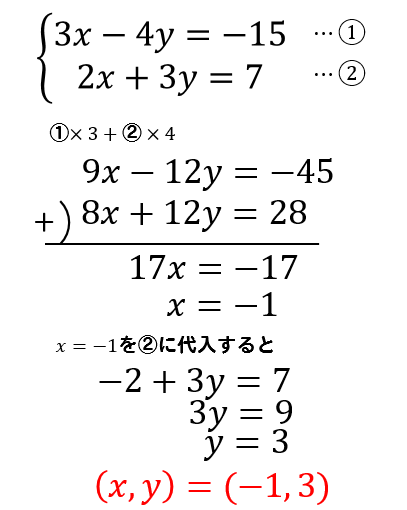 |  | |
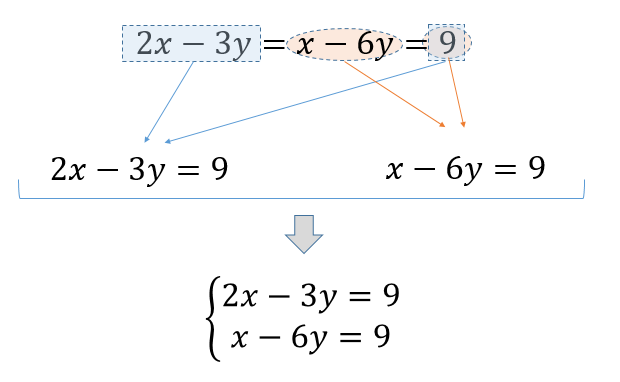 |  | |
 |  |  |
「連立 方程式 例題」の画像ギャラリー、詳細は各画像をクリックしてください。
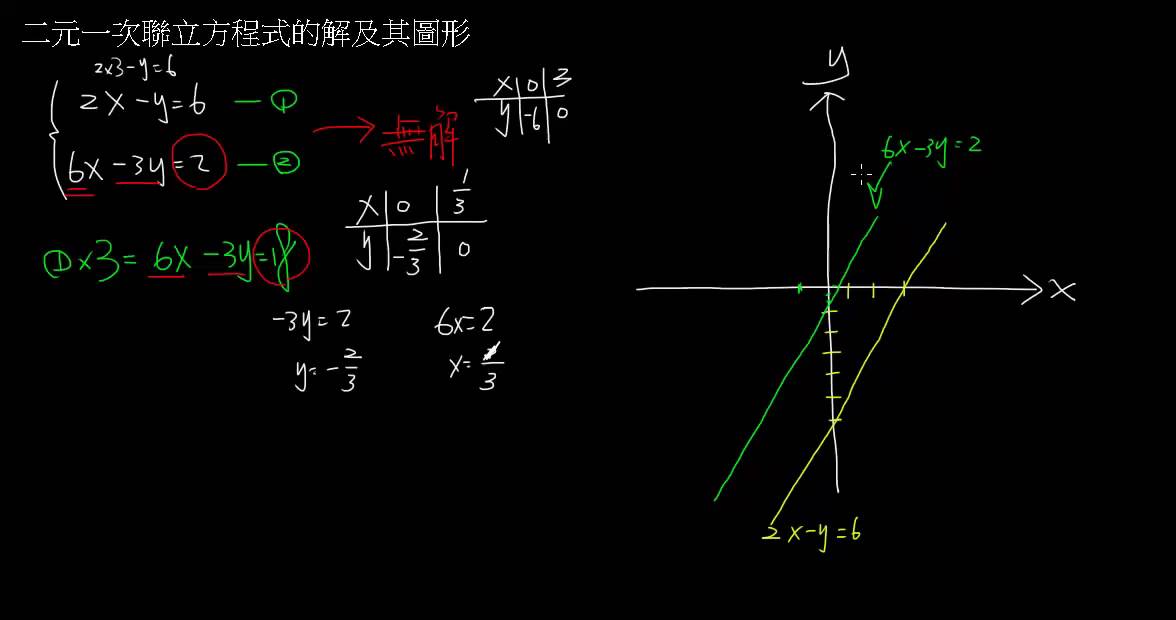 |  | |
 |  |  |
 |  | |
「連立 方程式 例題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  | 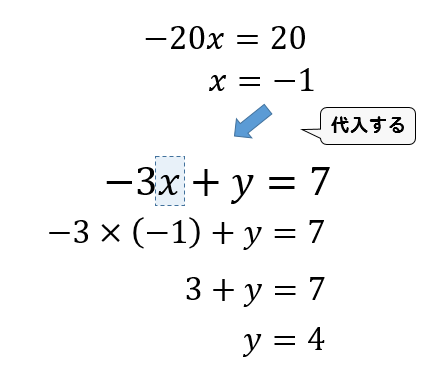 |
「連立 方程式 例題」の画像ギャラリー、詳細は各画像をクリックしてください。
 |  |  |
 |  |
6 文字の入った連立1 次方程式 例題5 以下の連立方程式が解を持つように,aを定めて解を求めよ. x y z= 6 x y 2z= 11 2x 2y− 4z= a (解答) 1 1 1 6 1 1 2 11 2 2 −4 a → 1 1 1 6 0 0 1 5 0 0 −6 a−12 → 1 1 0 1 0 0 1 5 0 0 0 a18連立方程式を解け x=2y5 x3y=7 x3y=7 x5y=11 2x3y=8 x5y=11 x2y=4 x3y=7 x2y=10 x=3y5 2x5y=11 3x4y=6 xy=10 x=y4 01x05y=13 03x04y=06 3xy=5 2 (x3y)=14 2 3 x 1 5 y= 8 15 2 5 x 3 10 y= 2 5 1 2 x 2 3 y= 1 6 3 2 x 7 6 y= 13 6 x3y=4x6y=2 解説リクエスト 解説リクエストフォーム 問題名
コメント
コメントを投稿